Dulce et utile

Dacă luăm două cuvinte monosilabice, mă și mai, observăm că timpul necesar pronunțării celui de-al doilea e mai lung decît în cazul primului (diftongul e echivalent cu o vocală lungă). Să ne imaginăm acum că avem un metronom: convenim că silaba scurtă cere o bătaie (o unitate de timp / o pulsație), iar silaba lungă cere două bătăi (două unități de timp / două pulsații). O silabă scurtă se va auzi natural mai slab decît una lungă, astfel că din alternanța lor va rezulta ritmul. Într-o poezie, dacă avem un vers compus din patru silabe, cum pot fi ele aranjate din perspectiva duratei? Dar dacă avem nouă silabe? Dar șaisprezece? Această problemă de combinatorică și-o pune, prin secolul II sau III î.Chr., matematicianul și poetul indian Pingala, cu privire la metrul sanscrit. El califică silabele drept „ușoare” și „grele” și formulează întrebarea generală: în cîte feluri poți aranja un număr n de silabe?
Dacă nu ai decît o unitate de timp, o poți umple doar cu o silabă scurtă, evident. Dacă ai două unități de timp, fie folosești două silabe scurte, fie una lungă (ss sau L). Dacă ai trei unități de timp, opțiunile sînt: fie trei silabe scurte, fie una scurtă și una lungă, fie invers – una lungă și una scurtă (sss, sL, Ls). Patru unități de timp (sau pulsații) se pot umple în cinci moduri: sss, LL, ssL, Lss, sLs. Și așa mai departe. Numărul de pulsații n este, teoretic, infinit, de aceea numărul de moduri în care ele pot fi aranjate în funcție de durată este o funcție: f(n) = f(n-2) + f(n-1). Dînd valori succesive lui n, Pingala obține un șir de numere (1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233...), o secvență stranie, în care fiecare număr din șir se obține adunînd cele două numere precedente. De la Pingala a rămas cel mai vechi tratat de prozodie sanscrită, Chandahśastra, al cărui titlu conține termenul chandaḥ, care înseamnă, printre altele, „metru poetic” și „frumos”, „plăcut”.
Curios la aceste numere este faptul că pot fi asociate cu lumea naturală. Ian Stewart spune, în Numerele naturii, că numărul de petale al aproape tuturor florilor se recrutează din seria 3 (crinii), 5 (piciorul-cocoșului), 8 (nemțișorii), 13 (gălbenelele), 21 (crizantemele), 34, 55, 89 (cele mai multe margarete). La floarea-soarelui, alveolele în care se găsesc semințele sînt aranjate în două familii de spirale care se intersectează; la unele specii, numărul spiralelor care se răsucesc în sensul acelor de ceasornic este de 34, iar în sens opus, 55; la altele sînt 55 și 89, sau chiar 89 și 144, toate numere consecutive în seria de mai sus. Ananasul are 8 rînduri de alveole dispuse spre stînga și 13 spre dreapta. Aceleași tipare spiralate pot fi identificate în conurile de pin sau într-o conopidă. Fiindcă la începutul secolului al XIII-lea seria lui Pingala a fost popularizată de matematicianul italian Leonardo Fibonacci (cel care a introdus și cifrele indo-arabe în Europa), ea e cunoscută sub numele de „șirul lui Fibonacci”, iar descoperirile devin din ce în ce mai interesante.
Dacă iei oricare două numere consecutive din șir, împărțindu-l pe cel mai mare dintre ele la celălalt, obții o constantă infinită: 1,6180339887... Mai scurt, 1,618 este „numărul de aur”, denumit phi (notat Φ) în cinstea lui Phidias, cel care a decorat Parthenonul cu sculpturi. Raportul dintre cele două numere este The Golden Ratio (GR), „proporția divină” sau „secțiunea de aur”, pe care o găsim ca principiu de construcție în Parthenon, în piramidele egiptene și în statuile antice. Picturile lui Da Vinci au GR ca bază a proporțiilor umane: dacă, de exemplu, împarți lungimea feței la lățimea ei, obții Φ. Dar tot corpul uman poate fi raportat numeric la seria Fibonacci și la numărul de aur – relația dintre număr și/sau mărime a oaselor, a dinților, a inimii, a creierului, a corpului calos. Inima bate în ritmul GR: raportul dintre sistolă și diastolă la tînărul sănătos este 1,61. Ramificarea ramurilor unui copac și a arterelor coronariene la om urmează o distribuție secvențială Fibonacci. Remarcabil, măsurătorile și găsirea unor proporții deviante pot ajuta în diagnosticarea timpurie a diverselor patologii. Cercetări comparatiste recente ale cercetătorilor de la Facultatea de Medicină a Universității Johns Hopkins, efectuate asupra unui lot de 100 de cranii umane și 70 de animale, arată că craniul uman respectă GR, spre deosebire de craniile de cîine, (două specii de) maimuță, iepure, leu și tigru. Mai mult, pe măsură ce gradul de sofisticare a unei specii crește, pe atît proporția se apropie de numărul de aur.
Dreptunghiul de aur este o figură geometrică cu laturile reprezentate de oricare două numere consecutive din seria Fibonacci – să zicem că lungimea are 34 cm și lățimea 21 (ca în desenul nostru). În interior trasăm pătratul cu latura de 21 cm și ne rămîne un dreptunghi cu laturile (13, 8). Desenăm în interiorul lui pătratul de latură 8 și ne rămîne un dreptunghi cu laturile (5, 3). Desenăm un pătrat de latură 3 și ne rămîne un dreptunghi cu laturile (3, 2). Desenăm un pătrat de latură 2 și ne rămîne un dreptunghi cu laturile (2, 1). Desenăm un pătrat de latură 1 și obținem încă un pătrat identic, de latură 1. Deci, în procesul invers, de compunere, nu de descompunere, desenul crește așa: 1, 1, 2, 3, 5, 8, 13, 21... ad infinitum. Acum: unind cu o linie unghiurile opuse ale tuturor pătratelor, obținem spirala de aur (vezi același desen), tipar care se regăsește în cochilia melcului, coada păunului, tentaculele caracatiței, mișcarea unui uragan, galaxii, cordon ombilical, ADN... spirala fiind cea mai eficientă formă de umplere a unui spațiu, așa cum au demonstrat matematicienii (în interior, simetria continuă: spiralele de nucleotide ale ADN-ului uman au proporții Fibonnaci, secțiunea transversală a dublei spirale ilustrează GR ș.a.m.d.).
În anii ’60, un strălucit lingvist american contemporan, Noam Chomsky, lucrînd pe terenul arid al sintaxei, propune o teorie absolut revoluționară care aduce împreună lingvistica, matematica, psihologia, biologia și, ultimativ, filozofia. Pornind de la faptul că sintaxa (felul în care sînt construite propozițiile și frazele) poate fi analizată matematic astfel încît să se identifice tiparele de organizare a vorbirii, Chomsky susține că acest demers ar putea dezvălui însăși organizarea mentală a facultății limbajului. Pornind de la un număr finit de sunete cu ajutorul cărora formează un număr finit de cuvinte, omul are, închis în cap, un mecanism care-i permite să înțeleagă și să genereze un număr infinit de mesaje. Această capacitate e centrală în teoria lui Chomsky, care o numește creativitate. Fiind o proprietate formală a sistemului sintactic, creativitatea chomskyană e de tip mecanic, fixată de reguli. (Celălalt sens pe care îl cunoaștem cu toții –„inventivitate”, „imaginație”, care sparge tiparele și încalcă regulile – e o proprietate a sistemului semantic, de care Chomsky nu e interesat). Mecanismul se bazează pe o gramatică universală, o teorie a gramaticilor, un fel de drivegenetic, o matrice cu setări și parametri activați și fixați de limba particulară la care omul este expus după naștere. Limbile naturale, deși diferite la suprafață, ar fi similare în adîncime, fiind modelate de structuri mentale inerente ființei umane, astfel că toate se supun constrîngerilor gramaticii universale, care specifică nu numai ce e posibil în limbă, dar și ce nu.
În virtutea acestui mecanism înnăscut, de a cărui prezență nu e conștient, omul adult e capabil nu numai de performanța menționată mai sus, ci și să recunoască (să „simtă”) dacă o înșiruire de cuvinte, deși absurdă, este corectă gramatical sau nu (Ideile verzi incolore dorm furios – așa sună celebrul exemplu chomskyan). Același mecanism (denumit LAD, Language Acquisition Device) permite ca, pe baza unui input sărac și nesistematizat, copilul mic să învețe limba maternă repede, însușindu-și, de fapt, un set de principii generale (reguli) care imprimă limbii capacitatea de autogenerare. Deși, prin gramatica sa transformațional-generativă, Chomsky descrie limba engleză cu ajutorul formulelor matematice (pe baza cărora putem azi „sta de vorbă” cu un chatbox), scopul final al alcătuirii unei gramatici generative este investigarea acestui LAD („organul limbii”, într-o exprimare metaforică). În această viziune, limba devine un produs natural, pentru că cele mai generale proprietăți structurale ale sale sînt determinate biologic.
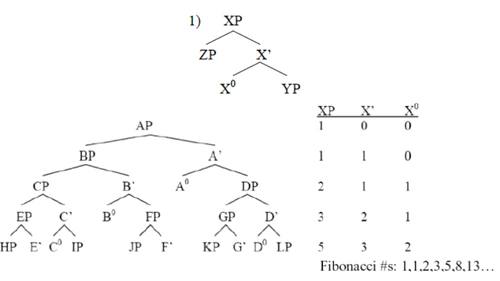
Atunci, seria Fibonacci are vreo relevanță în limbă? Investigații de ultimă oră în această direcție ar sugera că da. De exemplu, într-un studiu intitulat The Golden Phrase: Steps to the Physics of Language, David Medeiros și Massimo Piattelli-Palmarini, de la Universitatea din Arizona, analizează o anumită metodă de codificare a regulilor de construcție sintactică, numită the X-bar schema. Din păcate, nu există o terminologie corespondentă în limba română, studiile de acest fel, la noi, fiind inexistente; simplificînd la extrem, avem de-a face cu o rețetă binară de construire a grupului (phrase, XP) prin combinarea capului acestuia (the head, X⁰), mai întîi cu un alt grup (complement, YP), combinînd apoi rezultatul (X’) cu un al doilea grup (specifier, ZP). Așadar, cei doi observă că această schemă (a se vedea imaginea) constituie, de fapt, „un format recursiv absolut special”. The X-bar schema este identificată drept The Golden Phrase („grupul de aur”) „pentru că se asociază strîns cu numerele Fibonacci și GR”: repetată la infinit, schema produce, în generări succesive, seria Fibonacci în numărul fiecărui tip de grup (XP, X”, X⁰). Proprietățile schemei detaliate în studiu au fost considerate de Chomsky însuși, în mai multe conversații cu cei doi autori, „mai interesante decît cred ei”.
În teoria lingvistului american, capacitatea vorbitorului de a simți că o propoziție sau frază e rău construită (sau ceea ce vorbitorul știe despre limbă inconștient, fără a ști că știe, ca o intuiție) se numește competență (iarăși, un sens diferit de cel cu care sîntem obișnuiți). Punînd cap la cap toate cele de mai sus, putem întreba: dacă limba e un produs natural, iar biologia umană e dirijată de numărul de aur, am putea deduce că el explică originea competenței? Apoi putem extinde: nu cumva Phi și toate cele care rezultă din el sînt un „standard” care ne orientează inconștient întreaga activitate, nu numai pe cea lingvistică? Nu cumva, atunci cînd percepem ceva ca fiind frumos, o facem avînd acest substrat care ordonează percepția? Atunci, cele mai subiective impresii ar putea fi evaluate obiectiv, dacă am ști cum. Valabilitatea noțiunii de canon nu ar mai fi contestată. Frumosul nu ar mai fi în ochii privitorului, cum se spune. Arta nu ar mai fi o problemă de gust. Proporția divină se folosește, deja, în Vest, în operațiile estetice și în lucrările dentare cosmetice. Studiile asupra mersului uman arată că respectarea acestei proporții în fazele mersului nu se reflectă doar în armonia sa exterioară, ci și în eficiența consumului de energie, care devine optim. Trecînd la cealaltă extremă: am văzut că deviațiile de la GR se corelează cu diverse patologii în plan fizic. Nu s-ar putea oare ca și patologiile mentale să aibă la origine alterări interne ale acestui standard? Și întrebările pot curge avalanșă. Oricum ar fi, numerele lui Pingala/Fibonacci arată că dulce et utile, vechea aspirație a lumii antice către frumos și util, nu este doar o noțiune abstractă, ci o stare de lucruri, concretă și cît se poate de firească: armonia (frumusețea) și eficiența (utilitatea) coexistă și decurg una din cealaltă. Iar descoperirea altor moduri în care, vorba lui Eminescu, lumea și vecia se sprijină într-un număr e abia la început.
Laura Carmen Cuțitaru este conferențiar la Literele ieșene, specializată în lingvistică americană.








































